INDICE
1. Introduccion
2. Metodo de Euler
3. Metodo de Taylor
4.Metodos de Runge-Kutta
5. Conclusion
6. Bibliografias
INTRODUCCIÓN
Una EDO es una ecuación en qué las incógnitas son una o varias funciones que dependen de una variable independiente. Además, para evaluar la ecuación en un punto sólo nos hace falta conocer el valor de las funciones incógnitas y sus derivadas en ese punto. Otro tipo de ecuaciones no se llamarán ordinarias.
METODO DE EULER
h = xf - x0 / n
de manera que se obtiene un conjunto discreto de n+1 puntos: x0, x1, x3, ..., xn del intervalo de interes (x0, xf). Para cualquiera de estos puntos se cumple que:
xi = x0 + ih, .
METODO DE TAYLOR

METODO DE RUNGE-KUTTA
Entonces el método RK (de orden s) tiene la siguiente expresión, en su forma más general:
CONCLUSIÓN
Esta unidad mas pequeña, pero no por eso menos importante aquí se empleo conocimiento ya adquirido de otras unidades, algunos métodos que ya aplicamos en anteriores temas, así se concluye que los métodos están en nuestra vida diaria aunque no los veamos, estarán ahí por siempre.
BIBLIOGRAFIAS
https://www.sangakoo.com/es/temas/ecuacion-diferencial-ordinaria-edo
https://sites.google.com/site/metodosnumericosmecanica/home/unidad-vi/62-mtodos-de-un-paso-mtodo-de-euler-mtodo-de-euler-mejorado-y-mtodo-de-runge-kutta
https://www.monografias.com/trabajos91/metodo-series-taylor-resolver-ecuaciones/metodo-series-taylor-resolver-ecuaciones.shtml
1. Introduccion
2. Metodo de Euler
3. Metodo de Taylor
4.Metodos de Runge-Kutta
5. Conclusion
6. Bibliografias
INTRODUCCIÓN
Una EDO es una ecuación en qué las incógnitas son una o varias funciones que dependen de una variable independiente. Además, para evaluar la ecuación en un punto sólo nos hace falta conocer el valor de las funciones incógnitas y sus derivadas en ese punto. Otro tipo de ecuaciones no se llamarán ordinarias.
METODO DE EULER
En matemática y computación, el método de Euler, llamado así en honor de Leonhard Euler, es un procedimiento de integración numérica para resolver ecuaciones diferenciales ordinarias a partir de un valor inicial dado.
El método de Euler es el más simple de los métodos numéricos resolver un problema del siguiente tipo:
h = xf - x0 / n
de manera que se obtiene un conjunto discreto de n+1 puntos: x0, x1, x3, ..., xn del intervalo de interes (x0, xf). Para cualquiera de estos puntos se cumple que:
xi = x0 + ih, .
METODO DE TAYLOR

METODO DE RUNGE-KUTTA
El método de Runge-Kutta es un método genérico de resolución numérica de ecuaciones diferenciales. Este conjunto de métodos fue inicialmente desarrollado alrededor del año 1900 por los matemáticos C. Runge y W. Kutta.
Los métodos de Runge-Kutta (RK) son un conjuntos de métodos iterativos (implícitos y explícitos) para la aproximación de soluciones de ecuaciones diferenciales ordinarias, concretamente, del problema del valor inicial.
Sea
y´(t) = f (t, y (t))
una ecuación diferencial ordinaria, con  donde
donde  es un conjunto abierto, junto con la condición de que el valor inicial de ƒ sea
es un conjunto abierto, junto con la condición de que el valor inicial de ƒ sea
 donde
donde  es un conjunto abierto, junto con la condición de que el valor inicial de ƒ sea
es un conjunto abierto, junto con la condición de que el valor inicial de ƒ seaEntonces el método RK (de orden s) tiene la siguiente expresión, en su forma más general:
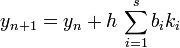 ,
,
donde h es el paso por iteración, o lo que es lo mismo, el incremento  entre los sucesivos puntos
entre los sucesivos puntos  y
y  . Los coeficientes
. Los coeficientes  son términos de aproximación intermedios, evaluados en ƒ de manera local
son términos de aproximación intermedios, evaluados en ƒ de manera local
 entre los sucesivos puntos
entre los sucesivos puntos  y
y  . Los coeficientes
. Los coeficientes  son términos de aproximación intermedios, evaluados en ƒ de manera local
son términos de aproximación intermedios, evaluados en ƒ de manera local
con  coeficientes propios del esquema numérico elegido, dependiente de la regla de cuadratura utilizada. Los esquemas Runge-Kutta pueden ser explícitos o implícitos dependiendo de las constantes
coeficientes propios del esquema numérico elegido, dependiente de la regla de cuadratura utilizada. Los esquemas Runge-Kutta pueden ser explícitos o implícitos dependiendo de las constantes  del esquema. Si esta matriz es triangular inferior con todos los elementos de la diagonal principal iguales a cero; es decir,
del esquema. Si esta matriz es triangular inferior con todos los elementos de la diagonal principal iguales a cero; es decir, 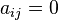 para
para  , los esquemas son explícitos.
, los esquemas son explícitos.
 coeficientes propios del esquema numérico elegido, dependiente de la regla de cuadratura utilizada. Los esquemas Runge-Kutta pueden ser explícitos o implícitos dependiendo de las constantes
coeficientes propios del esquema numérico elegido, dependiente de la regla de cuadratura utilizada. Los esquemas Runge-Kutta pueden ser explícitos o implícitos dependiendo de las constantes  del esquema. Si esta matriz es triangular inferior con todos los elementos de la diagonal principal iguales a cero; es decir,
del esquema. Si esta matriz es triangular inferior con todos los elementos de la diagonal principal iguales a cero; es decir, 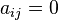 para
para  , los esquemas son explícitos.
, los esquemas son explícitos.CONCLUSIÓN
Esta unidad mas pequeña, pero no por eso menos importante aquí se empleo conocimiento ya adquirido de otras unidades, algunos métodos que ya aplicamos en anteriores temas, así se concluye que los métodos están en nuestra vida diaria aunque no los veamos, estarán ahí por siempre.
BIBLIOGRAFIAS
https://www.sangakoo.com/es/temas/ecuacion-diferencial-ordinaria-edo
https://sites.google.com/site/metodosnumericosmecanica/home/unidad-vi/62-mtodos-de-un-paso-mtodo-de-euler-mtodo-de-euler-mejorado-y-mtodo-de-runge-kutta
https://www.monografias.com/trabajos91/metodo-series-taylor-resolver-ecuaciones/metodo-series-taylor-resolver-ecuaciones.shtml


Comentarios
Publicar un comentario